menu
 |
 |
 |
 |
isolation, bruits
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
locaux d'écoute
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
isolation
acoustique des parois : parois simples, ne comportant qu'un seul matériau
En
bas de page, un résumé propose des conclusions simples,
dont on peut se contenter |
On
appelle paroi simple une paroi qui ne comporte dans son épaisseur qu'un
seul matériau, homogène ou à peu près, ayant
(forcément) une certaine masse,
en ne tenant pas compte de tout matériau de surface dont la masse
est faible
On néglige donc, parce que cela n'a aucun effet, tout revêtement
de surface de faible masse type peinture, papier, liège,
mousses diverses, textiles, laines minérales, etc, quelle que soit son épaisseur. |
Affaiblissement
et loi de masse
L'affaiblissement
est une grandeur qui caractérise la transmission directe à
travers une paroi voir transmission
du bruit
|
le coefficient
de transmission de la paroi est t = It / I
t est sans unité et << 1 en général
L'affaiblissement
de la paroi est R = L – Lt = 10 log 1/ t en dB
La fameuse
loi théorique
dite " loi de masse " affirme : R
= 19 log M + 20 log f/500
f est la fréquence du son .... rien à voir avec la paroi,
M est la masse surfacique de la paroi en Kg/m2.
La masse surfacique
est la masse par unité de surface, produit de la masse volumique
par l'épaisseur, cette relation n'a de sens que si M est constante
sur la surface de la paroi, donc paroi ne comportant qu'un seul matériau
homogène, d'épaisseur constante sur toute la surface.
En fait cette loi suppose pour être établie, et donc utilisée,
des conditions qui ne sont jamais réalisées en pratique,
elle n'est donc pas utilisable pour faire des calculs, elle conduirait
à des résultats erronés (et dans le mauvais sens).
Elle permet
néanmoins
de comprendre que l'affaiblissement R augmente avec la fréquence
(ce qui est facile à constater à l'oreille), et ne dépend
que de la masse, ce qui signifie que pour bien affaiblir les bruits, il
faut des parois, si elles sont simples, lourdes et épaisses |
|
Loi
pratique |
|
Dans
la pratique on constate que :
R réel < R théorique parce que les conditions ou hypothèses
de la loi de masse ne sont pas satisfaites; ces conditions sont :
· paroi totalement désolidarisée à sa périphérie
· paroi homogène dans l'épaisseur et sur sa surface
· matériau pas (ou peu) rigide
---> Tendre vers ces conditions entraine un meilleur comportement de
la paroi ...
ce qui n'est pas évident, mais signifie que la mise en oeuvre
influe beaucoup !
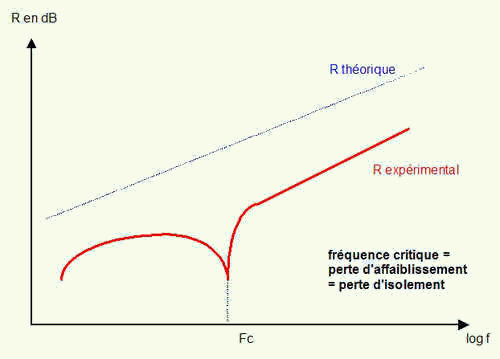
On constate
aussi que l'augmentation de l'affaiblissement R avec la fréquence ne
suit pas vraiment l'allure prévue par cette relation, et qu'il
existe une particularité gênante, c'est la fréquence
critique Fc, à laquelle (ou autour de laquelle) R a une valeur
faible.
Cette fréquence
critique Fc dépend du matériau, et de l'épaisseur
de la paroi :
Fc = Fc(1 cm) / e avec
e = épaisseur en cm
Fc(1cm) est très variable selon les matériaux, exemples
:
| verre 1200 Hz/cm |
plâtre
4200 |
acier 1200 |
| béton
2000 |
briques
2500
à 3500 |
bois
2000 à
3000 |
|
Comportement
particulier des parois
Ceci
explique que les comportements des parois sont extrèmement
différents, certaines ont des fréquences critiques
basses (maçonnerie
épaisse), d'autres des fréquences critiques élevées
(vitrages, bois faible épaisseur). et donc des courbes de variation
de R très différentes et parfois très "accidentées",
parce que les matériaux ne sont pas bien homogènes, ou
les
épaisseurs variables : il peut exister plusieurs fréquences
critiques. On
ne peut donc pas vraiment déterminer par calcul les affaiblissements,
il faut utiliser des résultats d'essais effectués en
laboratoire, et s'en servir en admettant des incertitudes liées aux
mesures et à la
mise en oeuvre.
On peut dire que les parois ont en quelque sorte leur "personnalité",
chacune a une capacité globale en fréquence d'affaiblissement
différente selon les spectres des bruits émis; on a
parfois l'impression que l'isolation est moins bonne pour certains
bruits que pour d'autres, ce n'est pas une impression ! |
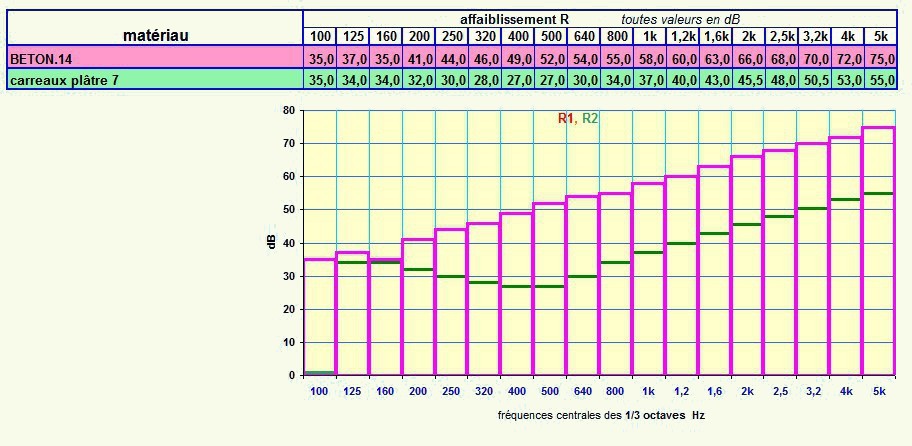
le
béton 14 cm a une masse surfacique de 300 kg/m2 et une fréquence critique
très basse, le phénomène est à peine visible sur la courbe; la paroi
en carreaux de plâtre a une masse surfacique de 72 kg/m2 et une fréquence
critique de 500 Hz environ
Affaiblissement
standardisé Rw
L'affaiblissement
Rw, souvent donné par les fabricants, est un affaiblissement
global, donc une valeur unique. Sa définition est issue
de la réglementation : il se calcule selon une méthode
normalisée à partir de la connaissance de la variation
de R en fonction de la fréquence. On trouve aussi l'indice
ancien R "global" en dBA, pratiquement égal
(1 dB d'écart en moyenne, statistiquement). Son utilisation
présente un intérêt essentiellement en conception
de logements neufs. Il permet aussi de comparer simplement 2
matériaux, mais ne donne pas la connaissance de la variation
de R en fonction de la fréquence.
voir d'autres exemples illustrant cette page par des données expérimentales
: affaiblissements 1/3 octaves en page
calculs
|
conclusions |
- L'affaiblissement d'une paroi représente sa capacité propre à diminuer
les bruits,
- une paroi simple ne comporte qu'un seul matériau dans son épaisseur,
en négligeant tout revêtement de surface de finition
de masse faible,
- dans une telle situation seule sa masse, c'est à dire la
densité du matériau et son épaisseur, a une
influence
|
- L'efficacité d'une
paroi simple augmente avec la fréquence : elle est plus
faible aux fréquences basses : toutes les parois
laissent mieux passer les sons graves,
- cette augmentation permettant d'atteindre des valeurs
intéressantes n'existe qu'au-dessus d'une fréquence
plutôt basse pour les parois épaisses, ce qui est favorable,
et moyenne pour les parois plus minces, voire assez élevée
pour les vitrages d'épaisseur courante,
- donc seules les parois simples porteuses, en maçonnerie,
pierres, etc, remplissent naturellement les conditions pour diminuer
de manière importante la transmission des bruits,
- la seule alternative possible est la paroi double
|
suite
: isolement
entre locaux |
|
|
Réalisé par Patrick Carré, ingénieur INSA, ancien acousticien conseil et prof acoustique Université Lyon
1
contact : 
La reproduction de tout ou partie de ce site sur tout document papier ou numérique est formellement interdite sauf avec l'autorisation de l'auteur, et sauf fiches pratiques |
|