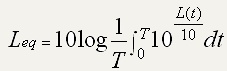menu
 |
 |
 |
 |
isolation, bruits
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
locaux d'écoute
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
bases de l'acoustique
:
niveaux sonores, perception des sons,
déciBels, déciBels
A, octaves |
loi
de la perception |
"la
sensation croit comme le logarithme de l’excitation" (loi
de Weber),
ce qui peut s'énoncer aussi : la sensation augmente comme se multiplie sa cause
Si on définit l'unité d'augmentation du bruit
comme correspondant à la multiplication par K de la puissance émise,
le bruit (ce que l'on entend) augmente d'autant à chaque
fois que la puissance est multipliée par K.
Non, la fonction log n'a pas été inventée
pour faire la sélection au bac, elle a des utilités!
Entre autres, d'expliquer le fonctionnement de notre système
auditif. C'est pourquoi (mauvaise nouvelle ...) on la retrouve
dans toutes les lois de l'acoustique. |
cause :
nombre de sources de bruit identiques
ou puissance acoustique émise |
sensation |
|
N |
A |

correspond
à multiplication par K de la cause |
N x K |
A+1 |
N x K x K |
A+2 |
N x K x K x K |
A+3 |
N x K x K x K x K |
A+4 |
|
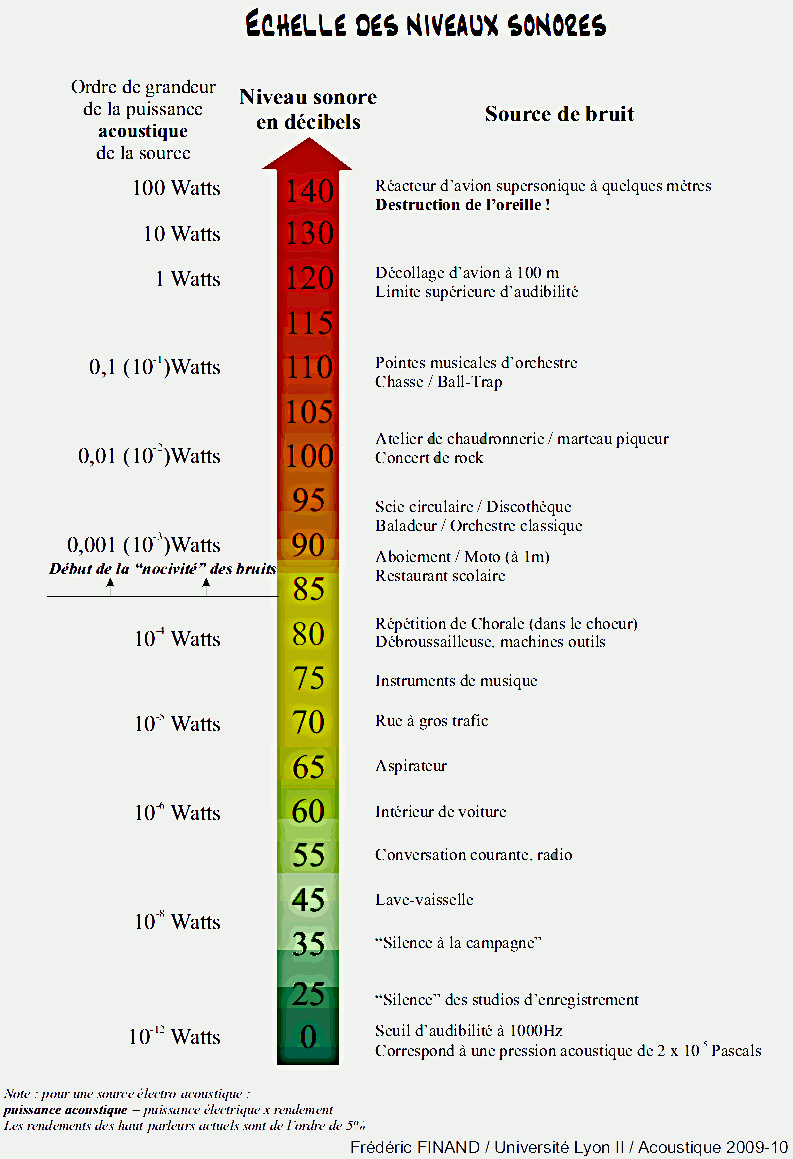
niveau
sonore en déciBels |

|
Ainsi L
= 0 dB correspond non pas à "pas de son ",
mais au bruit minimum (= seuil d'audibilité) que l'on
peut entendre
1 déciBel = 1/10 Bel (
le Bel n'est pas utilisé)
log = logarithme décimal
|
Cette valeur de po = 0 dB est extrèmement
faible : l'oreille est un capteur très sensible, très
performant, mais logarithmique.
La puissance acoustique est proportionnelle au carré de
la pression. On peut écrire L = 10 log (W / W0) avec
W0 = 10 puissance -12 watt.
Petit calcul avec la formule du niveau sonore : si l'on multiplie
la puissance par 2, L augmente de 3 dB.
On peut dire :"lorsque
la cause du bruit double, le bruit augmente de 3 dB" ...
Mais pas : "lorsque le bruit double" : le bruit, c'est ce que l'on
entend, ce sont les déciBels.
La cause, c'est l'énergie,
la puissance, le nombre de sources identiques.
Lorsqu'un fabricant écrit "mon produit divise le bruit par 2", cela signifie qu'il le diminue de 3 dB, ce qui est une "amélioration" extrèmement faible, à la limite de la perception !
|
|
octaves
et 1/3 d'octaves |
La loi de la perception s'applique à toute cause de sensation,
et donc aussi à la quantité fréquence.
Nous entendons les variations de la pression de l'air dont la
fréquence est comprise entre 20 Hz et 20000 Hz
On utilise donc toujours pour représenter des phénomènes
variables avec la fréquence (et ils le sont tous), une échelle
log,
permettant de satisfaire la condition :
est égal sur le papier (ou l'écran) ce qui est égal
pour l'oreille
On a définit des intervalles qui sont des divisions de
cette bande des fréquences audibles : l'octave et
le 1/3 d'octave
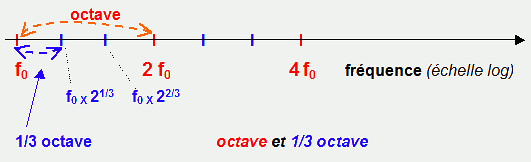
L'octave correspond à la multiplication
par 2 de la fréquence.
il y a 3 tiers d'octave dans 1 octave, donc le rapport des fréquences
limites du 1/3 d'octave est 2 puissance (1/3) .
L'origine du mot octave est qu'il est le 1/8 de la bande des fréquences
émises par les instruments de musique et audibles. |
 |
courbes
d'égale sensibilité |
|
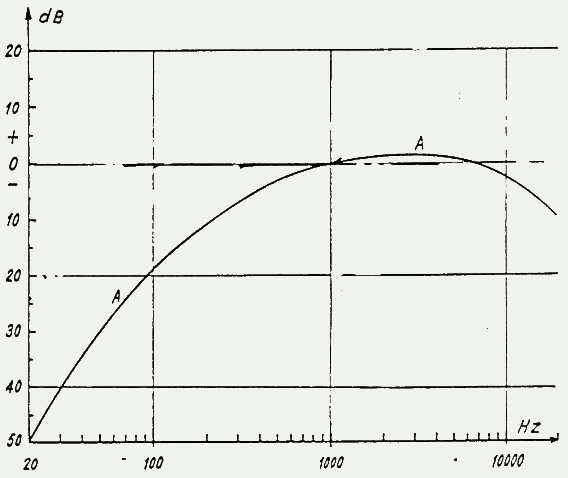
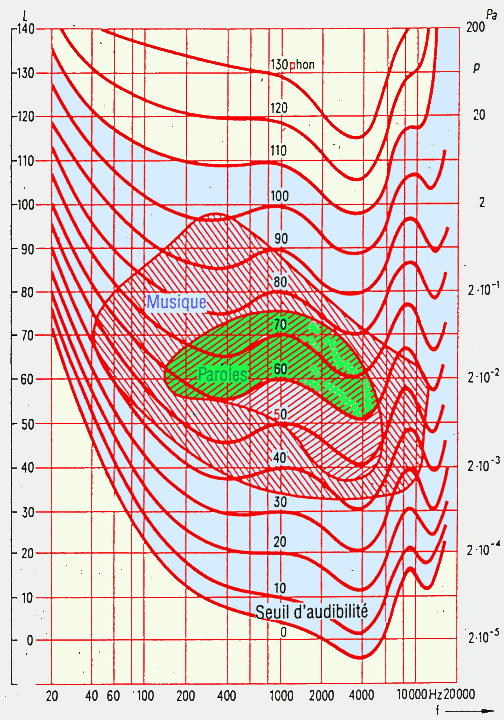
Ces courbes d'égale sensibilité représentent
en fait l'audiogramme d'un individu à l'audition normale.
Chaque ligne correspond à des sons "purs" (ne
comportant qu'une seule fréquence) reconnus comme étant
de même intensité., donc égaux en
"volume" pour l'oreille.
On constate que :
- lorsque le niveau est faible, on entend nettement moins bien
les sons les plus aigus et les plus graves (il en faut plus
pour entendre pareil)
- lorsque le niveau est élevé, des différences
moins importantes de perception existent à ces fréquences
- ce sont les sons les plus utiles à l'homme (dans l'histoire
de l'humanité) qui sont le mieux perçus, de 300 à 5000
Hz, ceux qui permettent la communication (paroles), la reconnaissance
des sons de la nature, cris d'animaux, etc
- la variation de l'allure des courbes en fonction du niveau
est modérée au-dessus de 1000 Hz, elles sont presque
parallèles
- elle est par contre très importante dans les fréquences
basses : on entend mal les sons graves à faible volume
- ce qui est une mauvaise chose pour l'écoute, de musique
par exemple, d'où l'existence de réglages "loudness", "physio", "bass
enhance", etc, sur les appareils de reproduction sonore
- mais ce qui est favorable quand il s'agit de bruit, car les
matériaux naturellement affaiblissent mal les fréquences
basses : en quelque sorte, notre oreille élimine ce que
les parois n'ont pas suffisamment fait ...
|
pondération
A |
La pondération A a été définie
par nécessité, lorsqu'on a voulu promulguer une
réglementation de l'isolation acoustique dans l'habitat
(1970), afin de tenir compte de cette réalité humaine
de la faible sensibilté aux bruits de basses fréquence.
Depuis, la quasi totalité des réglementations
l'ont adopté. Puis l'harmonisation européenne
a ajouté d'autres moyens (indice "W").
Elle est utilsée aussi bien pour faire des calculs prévisionnels
que des mesures, intégrée dans les appareils de mesure,
sonomètres et autres, logiciels de calcul.
Le but est d'obtenir une valeur unique de niveau sonore, prenant
en compte toutes les fréquences (presque) comme le fait
le système auditif. La courbe A (ci-contre) est une approximation
de l'inverse de la courbe d'égale sensibilité (ci-dessus)
passant par 30 dB à 1 kHz.
Dans le principe, elle est donc valable pour des niveaux faibles.
Ce qui est la réalité concernant les bruits reçus
dans un problème d'isolation, si cette isolation est correcte.
Ce n'est plus le cas si les niveaux sonores sont assez élevés.
Ce qui n'empêche que la pondération A est quand même
normalisée dans le cadre de réglementations concernant
des niveaux forts, par exemple celle limitant les "bruits" dans
les établissements diffusant de la musique (discothèques,
concerts) .
|
|
niveau
sonore global en dB et dBA |
Global signifie une seule
valeur, et non pas une courbe ou un
tableau de valeurs. Il y a donc 2
types de niveaux : globaux et variables en fonction de la fréquence.
Les niveaux en fonction de la fréquence sont représentés sous forme
de courbe ou de tableau.
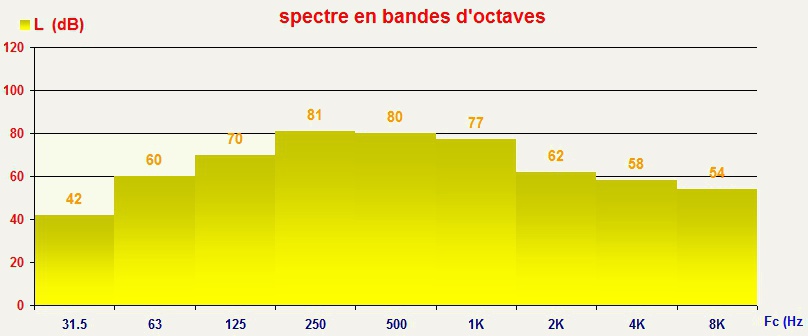
| La méthode pour obtenir un niveau global à partir
des valeurs par bandes consiste à effectuer la
"superposition" ou sommation logarithmique des
valeurs lues dans le tableau ou sur la courbe : |
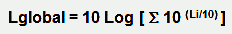 |
Pour un niveau global en dBA, d'abord ajouter algébriquement
la valeur obtenue sur la courbe de pondération à
celle du niveau par bande (octave ou 1/3), puis effectuer le calcul
du niveau global dBA avec la relation.
moyens de calcul et de
tracé : applications
Excel / Libre Office téléchargeables en
page calculs
- "analyse
spectrale" pemet à partir
des valeurs par bandes d'octave le tracé du spectre de
bruit et ce calcul automatique du niveau global pondéré A
et non pondéré.
- "analyse spectrale1-3",
idem à partir
des valeurs en 1/3 d'octaves, avec calcul intermédiaire des valeurs
par octaves.
|
bruits
variables : niveau équivalent Leq ou LAeq |
Pour
caractériser une nuisance due à une exposition de durée importante
à un bruit variable dans le temps, on utilise la notion de niveau
sonore équivalent (ou niveau sonore moyen) Leq, ou LAeq (en dBA).
Il est admis que, pour des bruits n'engendrant pas de lésions à court
terme du système auditif, cette quantité a une bonne
corrélation avec
les conséquences sur l'être humain, au sens large, des nuisances
sonores.
Le niveau sonore Leq est défini par :
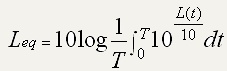 |
Cette formule parait a priori complexe
: l'expression après 10 log est la moyenne de la fonction
10 puissance (L/10), avec L variable en fonction du temps,
sur l'intervalle d'analyse T : la valeur du Leq est liée à une
durée d'exposition T.
On peut
démontrer que Leq est le niveau sonore constant qui
aurait nécessité la même énergie totale pendant l'intervalle
de temps considéré.
Il n'est jamais nécessaire de faire le calcul intégral, puisqu'on
ne connait pas la fonction mathématique L(t).
On appelle parfois
le Leq la "dose de bruit". |
La quantité se mesure directement avec un sonomètre
adapté, ou
après enregistrement, avec un logiciel spécialisé.
On peut aussi faire le calcul graphiquement, en traçant la courbe
L= f(t).
Le
Leq est utilisé, de manière réglementaire, pour des types de bruits
très différents :
- exposition aux bruits pendant les
périodes de travail, dans
l'industrie, sur les chantiers, etc : valeur maximale 85 dBA
sur toute la journée pour le travailleur (droit du travail)
- niveaux sonores dans
les "établissements diffusants
de la musique" ,
discothèques, lieux de concerts : maximum de 105 dBA sur
la durée de présence du public, en tout point accessible au public
- gêne due aux bruits de trafic
routier et ferroviaire : lorsqu'une
voie de circulation nouvelle est construite, elle ne doit pas
engendrer un Leq supérieur à 60 dBA
en façade (à l'extérieur) d'une habitation
en période de jour; la particularité des bruits de
trafic automobile est que la fonction L(t) est une loi statistique
("de
Gauss") qui a une moyenne et une distribution constante,
ce qui engendre qu'une mesure assez courte, de quelques minutes
selon le trafic, suffit pour obtenir un résultat reproductible,
et faire des comparaisons. Mais ce n'est pas le cas pour le trafic ferroviaire. Voir la page bruits
de trafic.
|
 autres
pages du site : textes
illustrés sur les thèmes de l'isolation acoustique,
de la qualité
des locaux d'écoute, et
sur les rapports entre acoustique
et sonorisation autres
pages du site : textes
illustrés sur les thèmes de l'isolation acoustique,
de la qualité
des locaux d'écoute, et
sur les rapports entre acoustique
et sonorisation |
|
|
|
Réalisé par Patrick Carré, ingénieur INSA, ancien acousticien conseil et prof acoustique Université Lyon
1
contact : 
La reproduction de tout ou partie de ce site sur tout document papier ou numérique est formellement interdite sauf avec l'autorisation de l'auteur, et sauf fiches pratiques |
|