acoustique des locaux d'écoute      isolation acoustique      son et acoustique
assistance pour la maîtrise de l'écoute

menu

les ondes stationnaires dans un local

Lorsqu'une onde sonore peut se réfléchir aux 2 extrémités d'un segment de propagation, il y a une superposition de 2 pressions de l'air, différentes en phase et presque identiques en valeur. S'il y a parfaite opposition de phase, cela se traduit par l'existence de "ventres" ou valeur maxi, et "nœuds" ou valeurs mini de pression, donc de niveau sonore.

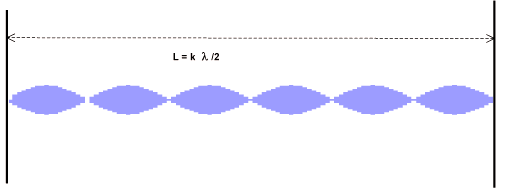
Dans le cas de 2 parois réfléchissantes parallèles, la condition est remplie si :
L = k l /2          k est un nombre entier, l est la longueur d'onde, L la distance
l = c / f      en mètres       f est la fréquence, c la vitesse du son c = 330 m/sec à 20°C et 1 bar, variable avec la température et la pression.

On nomme ondes stationnaires ces phénomènes. Les fréquences dites de résonance auxquelles elles se produisent sont donc :
fr = k ( 330 / 2 L)      fr en herz, L en mètres, k nb entier

Exemple : L = 5,00 mètres  fr = 33, 66, 99, 132, 165, 198 … Hz
Les ondes stationnaires sont d'autant plus gênantes qu'elles se produisent à des fréquences isolées : en se déplaçant dans le local, on remarque (c'est facile à l'oreille en émettant des sons sinusoidaux) des différences de niveaux très importantes entre 2 points distants de la demi longueur d'onde, 10 à 15 dB ne sont pas rares. Ceci est contraire à l'homogénéité de l'écoute, et peut aussi entrainer des vibrations d'objets divers variables selon les sons émis, et dépendant de leur emplacement. Il est facile en donnant à k les valeurs 1, 2, 3, 4, 5, etc, de constater que ces fréquences sont d'autant plus isolées dans le spectre qu'elles sont basses.
Dans l'exemple précédent, 33, 66, 132 Hz sont très gênants, puisqu'il y a un intervalle d'octave entre, une note correspondant à la fréquence fondamentale 66 Hz avec ses harmoniques à 132, 198 Hz, etc, aura un niveau énorme ou faible en des points distants de 2,50 m.


Pour les éviter, il faut :
· que les parois ne soient pas du tout parallèles ; et en plus ça ne suffit pas aux fréquences très basses, car les directions de réflexions sont assez quelconques.
· que l'une au moins des 2 soit absorbante à la fréquence considérée.
Il ne faut pas, en plus, que les ondes stationnaires existent aux mêmes fréquences dans plusieurs dimensions du local sinon les "creux et bosses" seraient énormes en niveau. Il existe un rapport idéal entre les 3 dimensions d'un local parallélipédique, tel que ces dimensions n'engendrent pas cette simultanéité (c'est le fameux "nombre d'or" des esthètes de la Renaissance italienne). Le pire est un rapport simple, par exemple 2,50 x 5,00 x 10,00 mètres, correspondant aux fréquences de l'exemple précédent.
Les locaux de grande qualité acoustique ont des formes évitant, et de loin, les parallèles, ce qui est une bonne solution.
Dans le cas le plus fréquent d'une salle existante ordinaire, un parallélépipède, on ne peut que réaliser une absorption sérieuse sur une des parois, aux fréquences les plus basses qui posent problème. voir matériaux absorbants

Voir en page calculs notre application excel Tr-optimat.xls qui, entre autres, calcule les fréquences des ondes stationnaires d'un local


suite :      matériaux absorbants         écoute et réverbération        traitement acoustique

 

l'analyse des phénomènes a été rédigée en espérant la rendre accessible à tout lecteur intéressé ...

mais avec une approche scientifique pour éviter les erreurs si courantes ...

 

acouphile.fr


site et outils de calcul réalisés par Patrick Carré, acousticien, ex prof ensam à l'IUT Lyon 1

avec la collaboration de Frédéric Finand, ingénieur du son, formateur   et responsable du studio de l'ENM de Villeurbanne.
Site de Frédéric :  oreilles délicates

 


dernière version :
4/09/10