menu
 |
 |
 |
 |
 |
isolation, bruits
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
locaux d'écoute
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
absorption
et réverbération du son |
absorption
et réflexion
|
|
 Il
ne faut pas confondre ABSORPTION et ISOLATION : l'absorption,
c'est a élevé,
ou Ir faible; l'isolation est importante si It est très faible.
Augmenter l'absorption, donc a, fait diminuer r, mais pas It ! L' absorption
est un phénomène de surface, et en général,
est obtenue avec des matériaux légers. L'isolation ne
peut être obtenue qu'avec de la masse, ou des couches multiples,
comprenant éventuellement un absorbant dans une lame d'air entourée
de part et d'autre d'éléments (au moins un peu) massifs.
L'absorbant absorbe s'il est placé en surface seulement,
et éventuellement
améliore l'isolation s'il est recouvert d'un matériau
massique, opaque, continu , mais alors il n'absorbe
plus dans le local. Voir isolation, parois
doubles.
La
réflexion se fait théoriquement de telle manière
que l’angle de réflexion est le même que l’angle
d’incidence par rapport au plan de l’obstacle. Mais lorsque
la surface de l’obstacle est accidentée le plan de surface
à considérer va dépendre du rapport entre la
taille des accidents de surface et la longueur d’onde. Lorsque
la longueur d’onde est de même taille que les irrégularités
de surface, il se produit un phénomène appelé «
diffusion ». L’énergie acoustique de l’onde
incidente est répartie dans de multiples directions : voir diffusion. |
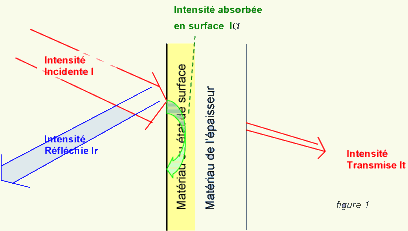
Lorsqu'une
onde sonore rencontre un matériau, une partie en général
importante de son intesité (ou de son énergie) est réfléchie
(donc si le matériau est une paroi, dans le même local
où
se trouve la source sonore); une partie en général très
faible est transmise à travers le matériau, et une dernière
partie est absorbée. Cette absorption est une transformation de
l'énergie acoustique en énergie mécanique (des mouvements,
déplacements, vibrations) et parfois calorifique, et a lieu essentiellement
en surface du matériau. N'oublions pas que les énergies acoustiques
sont toujours extrêmement faibles, donc les manifestations du phénomène
sont le plus souvent inférieures à
la limite de l'humainement perceptible. Nous verrons plus loin quels processus
peuvent engendrer cette transformation énergétique, donc
une absorption.
I = Ir + Ia
+ It It
<< I donc I = Ir + Ia (a
= alfa)
On
définit pour caractériser le phénomène
le coefficient d’absorption appellé généralement
alfa, ici on dira a = Ia / I , et de réflexion
r = Ir / I
On a donc : a + r = 1 car It / I pour une paroi est toujours < 0,01.
Un seul de ces 2 coefficients est nécessaire : c'est le coefficient d'absorption alfa = a
que l'on utilise, parce que la qualité correspond en général
à alfa élevé.
Pour connaitre les comportements des matériaux et les valeurs des coefficients alfa, voir matériaux
absorbant
|
réflexions
multiples dans un local |
Une
source sonore émet dans toutes les directions, d'une manière
plus ou moins régulière. La connaissance des caractéristiques
de directivité des sources est un élément important de la maitrise
de la répartition des sons dans une salle.
Intéressons-nous à la propagation d'une onde émise
dans une seule direction de l'espace à partir d'une source considérée
comme ponctuelle : on peut parler de "rayon" ou "vecteur"
acoustique.
|
|
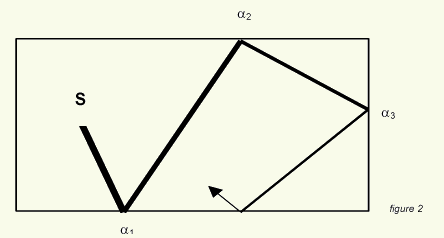
L'onde
sonore part de la source S, se propage en ligne droite jusqu'à
ce qu'elle rencontre une paroi : une absorption se produit, donc seulement
une partie (1 - alfa ) est réfléchie, se propage en ligne
droite, etc ….. au fur et à mesure de la propagation à
la vitesse de 330 m/sec (environ), donc du temps, peu à peu son
énergie diminue.
|
la
réverbération |
Considérons un
point M situé dans un local, et analysons ce qui s'y
produit lorsqu'on émet ailleurs une impulsion. Une impulsion est
un signal sonore très bref, produit par exemple par un choc sur
un objet résonnant, un claquement de main, un son de baguette
sur une caisse claire. |
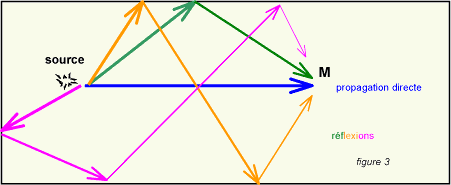
Le
premier (chronologiquement) "rayon" arrivant en M est celui
qui a parcouru la distance la plus courte, c'est celui qui s'est propagé
directement sans aucune réflexion, donc sans absorption. Puis arrivent
des rayons ayant suivi un trajet plus long, forcément avec une
réfléxion. Et ensuite, ayant subi de plus en plus d'absorptions.
Statistiquement, dans un local de forme simple, il est évident
que les rayons suivant des trajets de plus en plus longs, arrivant de
plus en plus tardivement, ont toutes les chances d'avoir subi plus de
réflexions, et donc si les coefficients d'absorption sont tous
du même ordre de grandeur, d'avoir des énergies de plus
en plus faibles.
Ces phénomènes sont rapides : à la vitesse de 330
m/sec, dans un local dont les dimensions sont de l'ordre de 10 mètres,
une trentaine de réflexions ont lieu en 1 seconde.
|
|
le
temps de réverbération Tr ou Rt60 |
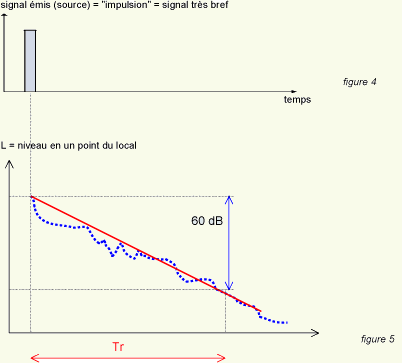
Si l'on
enregistre la variation du signal sonore en un point du local
après l'émission de l'impulsion, on constate :
· une décroissance qui peut en 1ère approximation
être assimilée à une droite ;
· que la pente de cette droite ne dépend (presque) pas du point
de mesure, elle est (presque) constante en tous points ;
· mais elle dépend (en général, beaucoup) de la
fréquence.
Dans
la plupart des différents domaines de l'Acoustique, on
caractérise le phénomène par la notion de Temps
de Réverbération, noté Tr en français
et RT60 en anglais. Tr est défini (voir schéma)
comme le temps en secondes mis par le signal pour décroître
de 60 dB (c'est à dire son énergie atteindre une
valeur 1000 fois plus faible).
Les valeurs de Tr usuellement constatées vont de quelques
1/10èmes à quelques secondes.
|
On constate facilement que la réverbération est très
importante dans des locaux grands, et dont les surfaces sont constituées
de matériaux lisses, durs, rigides, plans, comme béton,
pierres, carrelage, plaques métalliques, verre, et vides, sans
ou avec peu de meubles ou de personnes. par exemple : églises,
salles de sports, halls commerciaux d'aspect brut, stations de métro
anciennes, gares ….
On pourrait faire cette caractérisation par la pente de décroissance
en dB/seconde. On rencontre parfois cette notion, ainsi que celle de l' EDT (early decay time), qui est le temps correspondant aux 10 premiers
dB de décroissance.
|
Constatations expérimentales :
• linéarité
de la décroissance : · approximation qui dépend
de la fréquence
• indépendante du point de mesure ·
approximation, surtout
en fréquences basses
• vrai si :
local homogène et régulier, géométrie simple, matériaux
de surface régulièrement répartis
Lorsque les conditions
sont différentes, on trouve des décroissances en forme
de ligne brisée, avec des pentes variables entre le début
et la fin de la décroissance, des pentes dépendant
du point de mesure, surtout si les matériaux de surface ont
des coefficients d'absorption très différents entre
différentes zônes du local. Ceci est courant, et toujours
le cas dans les fréquences basses.
Un cas typique de géométrie engendrant ces réverbérations
non linéaires est la salle de spectacle avec scène, si la largeur
de l'ouverture entre les 2 parties est plus petite que la largeur des parties,
ou bien lorsque 2 locaux sont séparés par une grande porte ouverte.
voir écoute et réverbération
Il est pratiquement toujours impossible de mesurer une décroissance
de 60 dB, les méthodes manuelles ou les logiciels déterminent le Tr en
calculantt la pente de décroissance par une régression linéaire sur
la partie exploitable de la courbe, ou simplement en multipliant par
2 le temps d'une décroissance de 30 dB "judicieusement" choisie.
Il est donc clair que la notion, et donc les valeurs, du Temps de Réverbération,
sont des approximations, mais que l'on peut considérer comme suffisantes
pour traiter de nombreux cas.
|
calcul
du temps de réverbération Tr
|
De
nombreuses formules ont été établies pour lier
les valeurs de Tr aux caractéristiques de géométrie
et d'absorption des locaux. Il existe des formules anciennes, empiriques,
et des formules basée sur des raisonnements statistiques. La
plus ancienne est aussi la plus simple, et donc la plus largement
utilisée,
mais elle est relativement imprécise, et d'autant plus que alfa
est grand (10-15 % mini), c'est la célèbre
formule de Sabine. Sabine fut un acousticien pionnier américain. |
| formule
de Sabine : Tr
= 0,16 V/A |
V = volume en m3
A = "surface
d’absorption" du local en m2 = alfamoyen x S |
 |
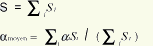alfa
i = ai = coefficient d’absorption "sabine"
du matériau i de surface Si
on peut trouver
des alfas "sabine" >1 |
| formule
d'Eyring : |
|
la formule de
Sabine est en fait une simplification de celle d'Eyring, en écrivant dans la relation alfa = - ln (1 - alfa),
donc la formule de Sabine, pratiquement toujours utilisée, est une approximation acceptable seulement si alfa moyen du local
faible. |
On
comprend donc que la réverbération est grande si le volume
est grand et / ou si l'absorption est faible.
Ces relations peuvent servir à déterminer Tr : il faut
connaître
les surfaces de tous les matériaux présents en surface
dans le local ( toutes les surfaces : murs, plafond, sol, objets divers
comme meubles), et leurs coefficients d'absorption respectifs, ce qui
peut être
assez compliqué. L'application Excel
/ Libre Office Tr-optimat téléchargeable en page calculs le
permet.
La formule
de Sabine sert aussi à calculer un coefficient d'absorption
en faisant 2 mesures de Tr : l'une dans un cas initial
à priori quelconque, la 2ème en introduisant dans le même
local une surface connue et suffisamment grande pour que la précision
soit acceptable, du matériau à étudier. Pour être
rigoureux on doit préciser en donnant une valeur de a ou alfa
la relation utilisée pour le calcul : on note "alfa sabine " ou "alfa
sab" ou "alfa s" ce coefficient. On définit
le coefficient d’absorption moyen du local, noté amoyen ou
am :
S = somme des surfaces "apparentes" du local (parois
et surfaces intérieures) : amoyen est une moyenne géométrique
On connaît alfamoyen par un calcul ou une mesure de Tr;
alfamoyen peut être considéré comme un simple
outil de calcul, une quantité "intermédiaire" simplificatrice.
Attention dans l'utilisation
de ces relations : TR, A, ai, alfamoyen sont toutes des quantités variables avec la fréquence.
|
|
 autres pages du site : textes
illustrés sur les thèmes de l'isolation acoustique,
de la qualité
des locaux d'écoute et sur
les rapports entre acoustique et sonorisation |
|
|
Réalisé par Patrick Carré, ingénieur INSA, EX prof acoustique IUT, licence Réhabilitation Bâtiments, Université Lyon
1,
conseil acoustique en Rhône Alpes
La reproduction de tout ou partie de ce site sur tout document papier ou numérique est formellement interdite sauf avec l'autorisation de l'auteur, et sauf fiches pratiques |
|
